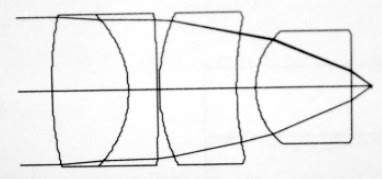
To change the diameter of a collimated laser beam, a simple type of Galilean telescope is used. Although a laser beam expander is nominally used on-axis, however if coma can be corrected, the system will be relatively insensitive to errors in alignment. For two-lens beam expander, two design parameters (i.e. the shapes of the two lenses) are available once the powers have been chosen. We might expect to be able to correct both the spherical aberration coefficient and coma coefficient.

Three-Lens Beam Expander
If a beam expander is composed of a plus-plus positive group. Then the coma is reduced. It can do better if the positive group is made from a plus-minus combination, in which the spherical aberration is correctable. To reduce the coma still further, we can split the two positive lenses, with a significant separation between them. It might be possible for the positive spherical aberration of the middle lens to correct the marginal ray height at the final lens.

F-Theta Lenses
Laser-printing systems generally require lenses with the property that the image size is proportional to the angle of the input beam, rather than to the tangent of this angle (which is common case when designing photographic lenses). These lenses are known as F-theta lenses. They always have an external pupil (the scanning mirror).
F-theta lenses often resemble one half of a double-Guass lens. In practice, a doublet does not provide enough parameters for an adequate F-theta lens, but a triplet would.

Lenses for Optical Disks
In optical disk players, a high-resolution lens is needed in order to read the data encoded on the disk. This lens must accurately follow the track that is recorded on the disk and therefore must be very lightweight. In practice the lenses are quite thick, and a useful improvement is obtained by the use of two aspherics.
Examples, the three-glass design by Sugiyama has a numerical aperture (NA) of 0.22 and the single aspheric lens by Arai et al has aspherics on both surfaces and a NA of 0.50. In laser physics, numerical aperture is defined slightly different, NA = n sinθ, where n is the index of refraction of the medium in which the lens is working (1.0 for air, 1.33 for pure water, and up to 1.56 for oils) and θ is the divergence of the beam. A Gaussian beam is formed as the lowest-order transverse mode in a stable laser resonator with spherical mirrors. The parameter of Gaussian beams are usually given at the 1/e fraction of maximum amplitude. The divergence of the beam is the far-field angle between the propagation direction and the distance from the beam axis for which the irradiance drops to 1/e^2 times the wavefront total irradiance.
Note: in most areas of optics, especially in microscope, θ is the half-angle of the maximum cone of light that can enter or exit the lens. In general, this is the angle of the real marginal ray in the system. In photography, instead of NA, angular acceptance of a lens is used. f/# = f/D, is the ratio of the focal length to the diameter of the entrance pupil. For small NA, f/# ~= 1 / 2NA. The f/# describes the light-gathering ability of the lens in the case where the marginal ray before (or after) the lens is collimated.
Sugiyama optical disk lens

Arai optical disk lens

Laser Diode Collimators
Since laser diodes produce a diverging beam, it is always necessary for the beam to be collimated. Collimators for laser diodes need to operate at high numerical apertures (about 0.60) to be compatible with the laser diode itself. In addition to the basic lens design (spherical aberration and coma), it is necessary to correct for the unequal divergence of the laser beam in the planes parallel and perpendicular to the emitting junction. Typically the beam widths in the two perpendicular directions are in the ration of about 2:1. Often this has to corrected so that the output beam from the collimator has a circular cross section rather than an elliptical cross section. This is commonly achieved by means of prisms arranged so that the beam diameter is increased in one direction.